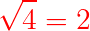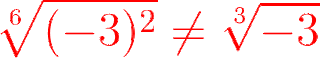Si alguna operación se puede considerar radical, en el sentido de revolucionaria, bien podría ser la de la raíz (o radical) de un número.
En principio se trata de obtener el número que elevado a un número da otro número determinado. Esto es,
entonces
Alguno ya se habrá dado cuenta que esta sólo es la mitad de la solución, pues podríamos tomar el valor (-2) como solución de la raíz cuadrada, ya que:
Y aquí ya empiezan los líos. Una operación matemática con dos soluciones, ¡pues vaya! Eso no ha gustado nada a los matemáticos de todos los tiempos.
Pero no nos vamos a adelantar. Primero te contaré cómo vamos a representar esta función tan peculiar:

- El número del cual queremos hallar la raíz se llama radicando,
- el número de veces que debemos multiplicar la solución de la raíz se llama índice
- y el resultado raíz o radical
A continuación, podemos deducir que la operación radical, sólo es otra forma de mirar a las potencias.
En efecto, si te das cuenta:
En este juego de potencias hemos encontrado que la operación radical es la que inversa de la operación potencia. Si suponemos que la operación radical es una especie desconocida de potencia, podemos concluir que equivale a hacer una potencia de exponente fraccionario cuyo denominador es el índice de la raíz. Esto es,
Si no te queda claro del todo piensa que para que los exponentes de la igualdad de arriba sean ciertos i/i =1, lo cual obliga a que la última igualdad sea cierta.
Ahora ya podemos concluir que las propiedades de los radicales son los mismos que las de las potencias equivalentes de exponente fraccionario (cuyo denominador es el índice).
Resumiendo:
- Radical de un radical con el mismo radicando es igual al radical de índice el producto de índices y como radicando, el común.
- Radical de un producto es el producto de radicales. Igual para las divisiones.
- El producto de radicales con radicando común es el radical de radicando común e índice la suma de los índices fraccionarios.
Si todavía no te ha explotado la cabeza, espera a ver lo que son los radicales equivalentes. En realidad no es muy raro si te digo que:
Dos radicales son equivalentes
si conducen al mismo resultado
Según las propiedades anteriores, podemos resolver distintos problemas:
- Introducir factores en un radical:
- Extraer factores en un radical:
Así, podemos usar estas operaciones para resolver productos de radicales con radicando e índice distintos, hallando radicales equivalentes con el mismo índice. Para ello el paso más importante es factorizar los números de forma que trabajemos sólo con números primos.
Terminamos este viaje con una paradoja. Relaja el cerebro y asómbrate ante el rincón más oscuro de las Matemáticas:
"Sabemos que
son equivalentes. Pero el radical de la izquierda produce dos resultados, uno positivo y uno negativo, al tener índice par. Mientras que el radical de la derecha produce un resultado positivo, por tener índice impar."
¿Cuál es el misterio?
Lo cierto es que estamos cometiendo una incorrección al realizar la simplificación de exponentes pues estamos olvidando las soluciones negativas. Esto sería cierto igualmente si el radicando fuera negativo, conduciendo a una incongruencia.
Como ves el tema de los radicales es complejo y sutil. Por ello trajo de cabeza a los matemáticos con estas y otras cuestiones, conduciendo a una región inhóspita en el siglo XVI como fue el campo complejo de los números radicales de índice par y radicando negativo.
Pero eso será otra historia. Mientras tanto no olvides enviar tus comentarios y correcciones.
J. Carlos Avendaño
Profesor e ingeniero