Comienza un nuevo día en la cueva y nuestra familia cazadora debe iniciar una peripecia en busca de comida. Los niños ya se levantan y empiezan a corretear por la estancia. Saber cuántos miembros hay en la familia, contando con los abuelos, primos y demás, es fundamental para aproximar la cantidad de comida que debemos traer. No sabemos cuántos amaneceres han transcurrido desde que nació el más pequeño de los cavernícolas pero seguro que en algunas más, estará listo para ayudar. Estas son una tarea de cálculo imposible sin tener unas herramientas que ayuden. Los números están a punto de nacer.
Aunque no tenemos constancia escrita de esta situación, nos podemos imaginar esta escena. Serán los babilonios y los egipcios los que dejen pruebas de la existencia de cálculos para su vida diaria a través de tablillas y papiros. Pero los griegos elevaron las Matemáticas a una categoría especial del conocimiento a través de la Geometría (“no entre nadie que no sepa Geometría”, era el lema de la academia de Platón).
Los números son herramientas mentales que los seres humanos utilizamos para expresar cantidades.
Durante más de 5.000 años los humanos hemos desarrollado diferentes tipos de números para expresar cantidades. Los números que usamos para contar se llaman naturales. Cuando introducimos la idea de deuda, o falta de algo, aparecen los números negativos, formando el conjunto de los enteros junto con los naturales. Al estudiar partes de una cantidad se encuentran los números racionales y, por oposición, los irracionales que no caben dentro de estos. Reuniendo a todos estos aparecen los números reales, que son los encargados de expresar cantidades en la vida real a partir de las operaciones básicas (suma, resta, multiplicación y división). Continuando con los números que generan negativos a partir de potencias pares, los llamados imaginarios o complejos, se obtienen la totalidad de los números conocidos.
LOS NÚMEROS NATURALES:
Los números naturales son los números que usamos para contar; uno, dos, tres, cuatro, etc, y fueron los primeros que se inventaron (o descubrieron, esa es una antigua discusión).
N= {1, 2, 3, 4, 5, 6, 7…}
Los números naturales fueron apareciendo poco a poco, según la necesidad, como demuestra la inexistencia de números en algunas civilizaciones. Por ejemplo, el cero fue una cantidad que fue admitida de forma tardía, al no representar ninguna cantidad. Los números a partir del 4 no existen en algunas civilizaciones por ser cantidades que no podemos contar instintivamente. En otras civilizaciones sólo existen tres números: el uno, poco y mucho. Muy sencillo pero poco exacto, ¿no crees?
Para más información sobre los números naturales consulta este enlace.
LOS NÚMEROS ENTEROS:
Cuando empezamos a operar con las cantidades nos encontramos que alguien nos debe dinero, o que falta una cantidad de sandwiches para alimentar a nuestros invitados o nos sobran tantos kilos para tener un cuerpo ideal.
La idea de quitar, asociada a la operación de diferencia o resta, supone la existencia de los números con signo negativo. A su vez, esto supone que los números naturales tendrían signo positivo. Uniendo estas ideas obtenemos los números con signo, el conjunto de los números enteros, llamado 
.
.
NÚMEROS RACIONALES:
Con la operación división, o cociente, ocurre como con la resta. Cuando operas dos números enteros, no siempre aparece otro número entero. Esto supone que si repartes 9 caramelos entre 4 amigos, no vas a poder repartir todos y darles la misma cantidad a cada uno. No hablemos si repartimos una tarta, ¿cómo expresamos la cantidad que resulta de repartirla entre los 30 compañeros de tu clase? De repente aparecen unas cantidades que no son enteras, sino fraccionarias y que se representan por los números racionales. Estos números resultan de dividir un entero entre otro entero.
= {m/n, m Z, n Z, n =0}
Sin tiempo para descansar a alguien se le ha ocurrido pensar si existen cantidades que no se puedan obtener mediante una división de enteros. ¡Pues sí!, son los números irracionales. A los pitagóricos les llevó a aborrecer cantidades tan endemoniadascomo las que se escondían detrás de la diagonal de un cuadrado de lado 1 o la relación entre una circunferencia y su diámetro.
Para más información sobre los números irracionales: Haz click aquí
NÚMEROS REALES:
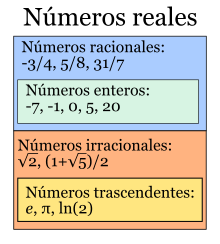
Si recogemos todos los números que ya conocemos (naturales, enteros, racionales e irracionales) formamos un conjunto mayor denominado el conjunto de los números reales, 
, posiblemente porque permite contar todas las cantidades que aparecen en la vida normal (¡o no!).
, posiblemente porque permite contar todas las cantidades que aparecen en la vida normal (¡o no!).
Antes de entrar en más profundidades vamos a descubrir un secreto oculto dentro de los números reales. Unos números que no se pueden expresar a partir de una expresión algebraica (o sea, un polinomio) con números racionales como coeficientes. Son los números trascendentes. Este conjunto de números son irracionales y poseen interesantes propiedades que los hace únicos.
Para más información sobre los números reales: Haz click aquí
NÚMEROS COMPLEJOS O IMAGINARIOS:
Si todos los números reales representan la vida cotidiana, ¿existen números más allá de los hacemos cada día? Esa pregunta tiene respuesta cuando nos planteamos otra pregunta: ¿qué número elevado al cuadrado tiene como resultado un número negativo? O bien, ¿cuál es la raíz cuadrada de menos uno?
El resultado fue bautizado por Euler como imaginario en el año 1777 y se le denominó i = √¯-1. Esta es la unidad que permite definir todas las raíces pares de los números negativos, números que existen en otro plano existencial distinto al de los reales. Auténticos fantasmas.
Estos fantasmas, junto con sus primos los números reales, permiten que cosas tan cotidianas como la electricidad de nuestra casa funcione correctamente.
Ya estamos en lo alto de los conjuntos numéricos, con los números complejos, que contienen los reales y los imaginarios. Con todos estos números podemos contar todas las cantidades que se nos ocurran y empezar a amar la rama de las matemáticas conocida como aritmética.
Para más información sobre los números complejos o imaginarios: Haz click aquí
Hasta ahora no se conocen más conjuntos de números, pero eso no quiere decir que no existan. ¿Te atreves a ser tú el descubridor del próximo conjunto numérico? Envíanos tu comentario y hagamos crecer el fabuloso mundo de las matemáticas.
J. Carlos y Belén Avendaño
No hay comentarios:
Publicar un comentario