MULTIPLICACIONES RECURRENTES

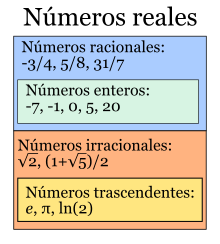
Existen multitud de ocasiones en que debemos multiplicar un número por sí mismo una cantidad determinada de veces... y esto es aburrido. Por ejemplo, el volumen de una caja de dimensiones iguales en altura, anchura y profundidad (dígase un cubo) es esa longitud multiplicada por sí misma tres veces.

Por ello, los babilonios en el siglo 18 A.C. ya pensaban en usar una operación denominada potencia para facilitar este cálculo. Consistía en multiplicar un número, llamado base, por sí mismo tantas veces como decía otro número, llamado exponente. Para los babilonios, y los árabes posteriormente, esta función se limitaba a las bases 2 y 3, que eran las más utilizadas.

En el siglo XVII, Descartes introdujo la notación actual para la función potencia que consiste en escribir el exponente en menor tamaño que la base y sobre él de la siguiente forma:

En este ejemplo hablaríamos de 2 elevado a 3 (o al cubo) y sería igual que multiplicar 2x2x2 = 8. Por ello es mucho más rápido hablar de potencias.

Aunque la base y el exponente pueden usar muchos tipos de número empezaremos por los números reales para la base y los enteros para el exponente.

La potencia se lleva bastante bien con el producto y la división. Por ello es interesante comprobar cómo se comportan estas operaciones entre sí.

Si una potencia se multiplica con otra potencia veremos que pasa. Existen tres casos:

1. Que las bases sean iguales: 

El producto de potencias de la misma base es igual a la base elevada a la suma de potencias

Esta propiedad es cierta también para el cociente de potencias de igual base.

2. Que los exponentes sean iguales:

El producto de potencias de igual exponente es igual al producto de las bases elevado al exponente común.

Esta propiedad es cierta también para el cociente de potencias de igual exponente.

3. Que ni exponente ni base sean iguales, con lo cual hay que calcular cada potencia por separado.

Además de estas propiedades conviene fijarse en la potencia de una potencia:

La potencia de una potencia es igual a la base elevada al producto de los exponentes.

Como puedes imaginarte ni la suma ni la resta de potencias se pueden simplificar en operaciones más sencillas (¡lo siento!).

Si el exponente tiene signo negativo, debemos suponer que algo cambia en la operativa. Efectivamente, ahora la potencia no consiste en una multiplicación repetida, sino una división repetida.

Así que, un exponente negativo en una potencia implica el inverso de la potencia. Conviene no confundir el inverso con el opuesto, la potencia negativa no cambia el signo del resultado (¡es un error muy habitual!).

Si ahora tomamos el producto de una potencia por ella con el exponente cambiado de signo (opuesto):

Al ser iguales ambas expresiones en su partida, son iguales en su resultado. Por tanto, cualquier número elevado a cero es igual a 1:

De esta forma puedes ver que un número, por grande que sea, elevado a cero siempre da uno.

En fin ya ves que el mundo de las potencias es apasionante y te lo puedes encontrar en los megas, gigas y teras de nuestros ordenadores cada día (¿sabes qué relación hay entre estas cantidades? Mira el enlace).

Por hoy esto es todo. No olvides enviar tus comentarios y continua tomando potencia hacia el mundo de las Matemáticas.

Un saludo.

J. Carlos Avendaño
Ingeniero y profesor

LOS DIVERSOS DISFRACES DE LAS FRACCIONES

Una fiesta elegante requiere un traje o un vestido deslumbrantes. Para hacer deporte nos ponemos ropa cómoda y zapatillas. Por la noche usamos un pijama o camisón (¡ya sé que existen versiones más ligeras!).

Igual que nosotros nos vestimos para la ocasión, nuestros amigos los números racionales (dígase, fracciones y enteros) se disfrazan según la situación. Quizás te sorprenda saber que 3/4, 0,75 o el 75% son distintas representaciones de la misma cantidad. Pues sí, nuestros amigos, los números racionales son muy coquetos.

En primer lugar hay que recordar que un número racional es aquel que se puede expresar como la división de dos números enteros.

Esto supone que 2/5 y 0,4 son la misma cantidad (lo puedes comprobar dividiendo 2 entre 5).

En algún momento de la Historia los pitagóricos se retorcieron de dolor cuando descubrieron que algunos números no se podían expresar como división de dos enteros. Por ejemplo el número PI o la medida de la diagonal de un cuadrado de lado 1 cm.

Siguiendo con nuestro baile de disfraces, nuestros amigos los números racionales se pueden poner serios en forma de fracción (1/2), informales en forma decimal (0,5) o elegantes en forma porcentual (50%).

Sí, todo esto está muy bien, pero ¿cómo cambiamos el disfraz a nuestros racionales amigos?

Como ya te conté, para pasar de fracción a decimal basta con dividir el numerador entre el denominador. Cuidado porque te pueden salir bastantes decimales. Por ejemplo, 1/3 tiene infinitos decimales que se repiten y vale 0,33333... (y así hasta el infinito). Esto lo representamos con un arco sobre el número que se repite (el periodo).

Para pasar de decimal a porcentaje sólo tienes que multiplicar la expresión decimal por 100. Esto significa expresar el número como la parte de una unidad (0,25 metros de 1 metro) o cómo la parte de una centena (25 metros de 100 metros, es decir, 25%).

Como ya puedes imaginar la parte difícil viene cuando tenemos que pasar de la expresión decimal a la fracción. En este caso tenemos que dividir los números decimales en tres tipos:

1. Los decimales exactos, que tienen un número de decimales concreto y finito. Por ejemplo 3,25 o 4,8.


2. Los decimales periódicos puros, que tienen un conjunto de decimales que se repiten de forma infinita. De este tipo son 3,222222.... y 21,345345345...


3. Los decimales periódicos mixtos, que tienen una parte decimal que no se repite y otra decimal que se repite infinitamente. Por ejemplo, 2,1455555... ó 32,456565656...

Para cada caso usamos un sistema distinto:

1. Los decimales exactos, tomamos todas las cifras y dividimos por un número formado por un 1 y tantos ceros como decimales.


2. Los decimales periódicos puros, tomamos las cifras y le restamos la parte periódica para conseguir el numerador. En el denominador se coloca un número con tantos nueves como cifras formen el periodo. Al final hay que obtener la fracción equivalente con el numerador y denominador más pequeños (fracción irreducible).


3. Los decimales periódicos mixtos, como antes el numerador será la resta de un número formado por las cifras menos la parte no periódica y periódica. El denominador se forma con un número formado por tantos nueves como cifras periódicas y tantos ceros como no periódicas. Nuevamente hay que reducir la fracción a su versión irreducible.

Para conocer la deducción de estas fórmulas generatrices te dejo el siguiente enlace donde podrás saber de dónde vienen.

Como ves los números racionales son muy coquetos y se visten de la mejor manera posible según la ocasión. Aprende a ponerles su traje adecuado en cada caso para que sean tus mejores amigos. Y no olvides dejar tus comentarios. 

LOS PRIMOS SON LOS LADRILLOS DE LOS NÚMEROS

Un descubrimiento sorprendente para los matemáticos fue darse cuenta que todos los números naturales se pueden construir como el producto de otros números especiales.

Primero vamos a buscar a estos "ladrillos" del resto de los números. Se trata de un grupo de números que no son divisibles entre ningún otro. Más correctamente, sólo se pueden dividir entre uno y entre ellos mismos, pero eso ya os lo podíais imaginar. Estos números se han llamado números primos.

Pues bien, cualquier número natural se puede construir mediante multiplicación de algunos números primos (sus factores). Este es el Teorema Fundamental de la Aritmética. Pero además, es que esta descomposición es única, es decir, sólo estos números primos pueden formar el número natural buscado. La demostración de este teorema es compleja pero la puedes consultar en el enlace anterior.

Como ya sabemos que todo número natural se puede obtener mediante el producto único de varios números primos, podemos hacer este proceso de descomposición de cada número en sus factores primos. A esto lo llamaremos "factorización".

Factorizar un número es hallar el producto único de sus factores primos.

Para ello probaremos dividiendo el número natural entre los números primos hasta encontrar uno que lo divida con resto cero (entre el que sea divisible). Una buena lista es la que encontrarás en este enlace.

De forma práctica sólo necesitas recordar los primeros números primos:

2, 3, 5, 7, 11, 13

Recuerda que un factor primo puede aparecer varias veces, por lo que conviene empezar siempre probando la divisibilidad desde el último factor hallado. Esto quiere decir que si 3 es factor de un número, habrá que empezar probando de nuevo si 3 es factor del cociente del número entre 3.

Esta operación, que acabamos de aprender, nos servirá para hallar ciertos números especiales que nos ayudarán a sumar fracciones, ordenarlas y encontrar cantidades que resuelven problemas sobre el uso de menos piezas.

Me refiero a los problemas de máximo común divisor (Mcd) y mínimo común múltiplo (mcm). Pero eso será otra historia, y debe contarse en otro momento.

Os dejo algunas factorizaciones de números para que practiquéis:

2	=	PRIMO
3	=	PRIMO
4	=	2 x 2
5	=	PRIMO
6	=	2 x 3
7	=	PRIMO
8	=	2 x 2 x 2
9	=	3 x 3
10	=	2 x 5
11	=	PRIMO
12	=	2 x 2 x 3
13	=	PRIMO
14	=	2 x 7
15	=	3 x 5
16	=	2 x 2 x 2 x2
17	=	PRIMO
18	=	2 x 3 x 3
19	=	PRIMO
20	=	2 x 2  x 5
21	=	3 x 7
22	=	2 x 11
23	=	PRIMO
24	=	2 x 2 x 2 x 3
25	=	5 x 5
26	=	2 x 13
27	=	3 x 3 x 3
28	=	2 x 2 x 7
29	=	PRIMO
30	=	2 x 3 x 5

No olvides enviar tus comentarios para mejorar esta entrada y así ayudar a muchos otros estudiantes con esta tarea.

TROZOS, PORCIONES, CACHOS: FRACCIONES DE VERDAD

Era el décimo cumpleaños de Elena y llegaba el momento de soplar las velas y abrir los regalos. ¡Qué emoción!, estaría la Nintendo entre aquellas cajas de colores. ¡O tal vez un teléfono móvil para conectarse por Whatsapp con los amigos!

La tarta con diez velas hizo su aparición y los 7 amigos soplaron al son del "Cumpleaños Feliz". Mientras Elena abría los regalos en busca de sus preciados objetos de deseo, su madre se esforzaba en cortar 10 trozos perfectamente iguales.

Mientras Elena abría los regalos, el padre de ella se comía los restos que sus amigos no querían, llegando a contarse 4 entre los trozos que engulló. Después tuvo que tomar una pastilla para el dolor de tripa por el empacho.

En esta historia aparecen las fracciones como partes de algo más grande. El reparto de un objeto supone dividirlo en partes iguales. El número de partes entre las que se divide (los invitados al cumpleaños) es el denominador. La cantidad de trozos que se come cada uno el numerador (cuatro en el caso del padre de Elena).

Por arte de magia las fracciones se pueden expresar de distintas formas ya que 4/10 es lo mismo que 2/5. Es decir que la cantidad de tarta que se comió el padre de Elena es igual que tomar cuatro partes si la tarta se divide en 10 o 2 partes si la tarta se divide en 5.

Esto se consigue dividiendo numerador y denominador por el mismo número (algún factor común de ambos) de forma que sean lo más pequeños posibles. De este modo obtenemos "fracciones equivalentes".

Las fracciones y los porcentajes están muy relacionados pues los porcentajes son fracciones donde el denominador (el número de veces en que partimos el objeto) siempre es 100. Así, cuando veas que tu pantalón favorito está rebajado un 25% piensa que el precio se ha repartido en cien partes y le han quitado veinticinco (¡eso es una pasta!).

Para comparar fracciones vamos a utilizar fracciones equivalentes con el mismo denominador de forma que sólo tendremos que comparar los numeradores. Si te dicen que te dan 2/5 de 100 euros o 3/7 de 100 euros, debes usar un denominador común. Esto equivale a comparar 14/35 con 15/35, donde puedes deducir que te interesa más tomar 3/7 (ó 15/35).

Para sumar y restar haremos igual que antes y usaremos fracciones equivalentes para operar nuestros números racionales. De esta forma sumaremos (o restaremos) los numeradores de las fracciones equivalentes y obtendremos la solución.

La multiplicación es sencilla, pues sólo tenemos que multiplicar el numerador de una fracción con el de otra y los denominadores entre sí.

La división es una multiplicación cruzada, donde el numerador del resultado es el producto del numerador de la primera fracción con el denominador de la segunda. El denominador del producto será el producto del denominador de la primera fracción con el numerador de la segunda. Es decir, una multiplicación "en cruz".

Sólo me queda recordarte la regla de oro de las fracciones:

"SIEMPRE TRABAJA CON LA FRACCIÓN MÁS SIMPLE DE LAS EQUIVALENTES"

De esta forma te evitarás muchos cálculos y su expresión es más fácil de recordar.

Espero que te haya ayudado con la operativa de fracciones y no olvides enviar tus comentarios o dudas.

J. Carlos Avendaño

Ingeniero y profesor

LA MAGIA DE LOS NÚMEROS A LO LARGO DE LA HISTORIA

Comienza un nuevo día en la cueva y nuestra familia cazadora debe iniciar una peripecia en busca de comida. Los niños ya se levantan y empiezan a corretear por la estancia. Saber cuántos miembros hay en la familia, contando con los abuelos, primos y demás, es fundamental para aproximar la cantidad de comida que debemos traer. No sabemos cuántos amaneceres han transcurrido desde que nació el más pequeño de los cavernícolas pero seguro que en algunas más, estará listo para ayudar. Estas son una tarea de cálculo imposible sin tener unas herramientas que ayuden. Los números están a punto de nacer.

Aunque no tenemos constancia escrita de esta situación, nos podemos imaginar esta escena. Serán los babilonios y los egipcios los que dejen pruebas de la existencia de cálculos para su vida diaria a través de tablillas y papiros. Pero los griegos elevaron las Matemáticas a una categoría especial del conocimiento a través de la Geometría (“no entre nadie que no sepa Geometría”, era el lema de la academia de Platón).

Los números son herramientas mentales que los seres humanos utilizamos para expresar cantidades.

Durante más de 5.000 años los humanos hemos desarrollado diferentes tipos de números para expresar cantidades. Los números que usamos para contar se llaman naturales. Cuando introducimos la idea de deuda, o falta de algo, aparecen los números negativos, formando el conjunto de los enteros junto con los naturales. Al estudiar partes de una cantidad se encuentran los números racionales y, por oposición, los irracionales que no caben dentro de estos. Reuniendo a todos estos aparecen los números reales, que son los encargados de expresar cantidades en la vida real a partir de las operaciones básicas (suma, resta, multiplicación y división). Continuando con los números que generan negativos a partir de potencias pares, los llamados imaginarios o complejos, se obtienen la totalidad de los números conocidos.

LOS NÚMEROS NATURALES: 

Los números naturales son los números que usamos para contar; uno, dos, tres, cuatro, etc, y fueron los primeros que se inventaron (o descubrieron, esa es una antigua discusión).

   N= {1, 2, 3, 4, 5, 6, 7…}

Los números naturales fueron apareciendo poco a poco, según la necesidad, como demuestra la inexistencia de números en algunas civilizaciones. Por ejemplo, el cero fue una cantidad que fue admitida de forma tardía, al no representar ninguna cantidad. Los números a partir del 4 no existen en algunas civilizaciones por ser cantidades que no podemos contar instintivamente. En otras civilizaciones sólo existen tres números: el uno, poco y mucho. Muy sencillo pero poco exacto, ¿no crees?

Para más información sobre los números naturales consulta este enlace.

LOS NÚMEROS ENTEROS:

Cuando empezamos a operar con las cantidades nos encontramos que alguien nos debe dinero, o que falta una cantidad de sandwiches para alimentar a nuestros invitados o nos sobran tantos kilos para tener un cuerpo ideal.

La idea de quitar, asociada a la operación de diferencia o resta, supone la existencia de los números con signo negativo. A su vez, esto supone que los números naturales tendrían signo positivo. Uniendo estas ideas obtenemos los números con signo, el conjunto de los números enteros, llamado .

NÚMEROS RACIONALES:

Con la operación división, o cociente, ocurre como con la resta. Cuando operas dos números enteros, no siempre aparece otro número entero. Esto supone que si repartes 9 caramelos entre 4 amigos, no vas a poder repartir todos y darles la misma cantidad a cada uno. No hablemos si repartimos una tarta, ¿cómo expresamos la cantidad que resulta de repartirla entre los 30 compañeros de tu clase? De repente aparecen unas cantidades que no son enteras, sino fraccionarias y que se representan por los números racionales. Estos números resultan de dividir un entero entre otro entero.

= {m/n, m Z, n Z, n =0}

Sin tiempo para descansar a alguien se le ha ocurrido pensar si existen cantidades que no se puedan obtener mediante una división de enteros. ¡Pues sí!, son los números irracionales. A los pitagóricos les llevó a aborrecer cantidades tan endemoniadascomo las que se escondían detrás de la diagonal de un cuadrado de lado 1 o la relación entre una circunferencia y su diámetro.

Haz click aquí para ver un video sobre los números racionales

Para más información sobre los números irracionales: Haz click aquí

NÚMEROS REALES:

Si recogemos todos los números que ya conocemos (naturales, enteros, racionales e irracionales) formamos un conjunto mayor denominado el conjunto de los números reales, , posiblemente porque permite contar todas las cantidades que aparecen en la vida normal (¡o no!).

Antes de entrar en más profundidades vamos a descubrir un secreto oculto dentro de los números reales. Unos números que no se pueden expresar a partir de una expresión algebraica (o sea, un polinomio) con números racionales como coeficientes. Son los números trascendentes. Este conjunto de números son irracionales y poseen interesantes propiedades que los hace únicos.

Para más información sobre los números reales: Haz click aquí

NÚMEROS COMPLEJOS O IMAGINARIOS:

Si todos los números reales representan la vida cotidiana, ¿existen números más allá de los hacemos cada día? Esa pregunta tiene respuesta cuando nos planteamos otra pregunta: ¿qué número elevado al cuadrado tiene como resultado un número negativo? O bien, ¿cuál es la raíz cuadrada de menos uno?

El resultado fue bautizado por Euler como imaginario en el año 1777 y se le denominó i = √¯-1. Esta es la unidad que permite definir todas las raíces pares de los números negativos, números que existen en otro plano existencial distinto al de los reales. Auténticos fantasmas.

Estos fantasmas, junto con sus primos los números reales, permiten que cosas tan cotidianas como la electricidad de nuestra casa funcione correctamente.

Ya estamos en lo alto de los conjuntos numéricos, con los números complejos, que contienen los reales y los imaginarios. Con todos estos números podemos contar todas las cantidades que se nos ocurran y empezar a amar la rama de las matemáticas conocida como aritmética.

Para más información sobre los números complejos o imaginarios: Haz click aquí

Hasta ahora no se conocen más conjuntos de números, pero eso no quiere decir que no existan. ¿Te atreves a ser tú el descubridor del próximo conjunto numérico? Envíanos tu comentario y hagamos crecer el fabuloso mundo de las matemáticas.

J. Carlos y Belén Avendaño